§A. Glossary
| Accretion.
| The process of gravitationally capturing matter.
|
| Advection.
| A non-circulatory redistribution of matter.
|
| Anisotropic.
| The property of being non-uniform.
|
| Apgalacticon.
| The most distant point of an object's orbit from the center of a galaxy.
|
| Barycenter.
| The center of mass of a system of objects.
|
| Big Bang.
| The most commonly accepted cosmological theory according to which the universe began in an enormous explosion 15 billion years ago.
|
| CDM. |
Abbreviation for Cold Dark Matter.
|
| Commensurabilities.
| The resonances formed between orbiting bodies whose orbital periods differ by an small integral amount.
|
| Dispersion.
| Scattering of values from an distribution's average.
|
| Dissipative.
| The property of dissipating or releasing energy.
|
| Galactocentric.
| A coordinate system centered on the galactic core.
|
| HI.
| Neutral atomic hydrogen.
|
| Hubble Constant.
| The constant of proportionality relating the recessional velocity of galaxies to their distance. The reciprocal of the Hubble Constant is the age of the universe, or Hubble Time.
|
| Inclination.
| The angle between the orbital plane of a satellite and the normal plane.
|
| Isophote.
| A contour of equal luminosity.
|
| LMC. |
Abbreviation for the Large Magellanic Cloud.
|
| Magnitude.
| A logarithmic measure of an object's luminosity.
|
| Maxwell distribution.
| Statistical distribution of particle velocities in a system in thermodynamic equilibrium.
|
| Milky Way.
| The name given our galaxy, also the Galaxy.
|
| Nutation.
| The periodic variation of the inclination of a gyroscope to the vertical.
|
| Oblate.
| A sphere flattened at the poles.
|
| Parallax.
| The displacement of an object, relative to a fixed background, due to the change in position of the observer.
|
| Perigalacticon.
| The closest point of an object's orbit from the center of a galaxy.
|
| Precession.
| The slow gyration of the rotation axis of a spinning body.
|
| QSO. |
Abbreviation for Quasi-Stellar Object or Quasar. A distant class of high energy objects thought to be young galactic nuclei.
|
| Radial velocity.
| The component of velocity along the observer's line of sight.
|
| Redshift.
| The shift of spectral lines towards longer wavelengths due to the Doppler effect or cosmic expansion.
|
| Resonance.
| The selective response of an oscillating system to an external oscillation at a frequency equal to some fraction of the natural frequency.
|
| Satellite.
| The name given to the smaller body orbiting a larger body.
|
| Tri-Axial.
| The property of having three distinct kinematic axes.
|
| |
§B. Units
and Terminology
The standard metric prefixes employed are from the Greek: kilo,
thousand; mega, million; giga, billion. An alphabetical
list of potentially unfamiliar terms appears in Appendix A.
Distance. The base unit of distance in galactic measurements
is the parsec. One parsec is 3.26 light years, defined
as the distance at which an object subtends one arc-second of
parallax, seen from the baseline of the earth's orbit. The kiloparsec,
or kpc, is used to describe the sizes of galaxies and the
megaparsec, or Mpc, to describe the distances between galaxies.
Time. A Hubble time is the age of the universe,
somewhere between 10 and 20 billion years (its specific value
is a matter of no little dispute). In this paper I take the Hubble
time to be 15 billion years. A common time scale, when discussing
galactic features, is a billion years, or a gigayear, abbreviated
Gyr. A Gyr is a little less than a tenth of the age of
the universe. Both distance and time are parameterized by the
redshift, or z. The redshift is defined as 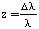 ,
the change in the wavelength over the wavelength itself. For
very distant objects, the expansion of the universe causes a lengthening
in the wavelength of light we see; a longer wavelength means a
shift towards the red end of the spectrum, hence redshift. The
most distant galaxies we observe are at z = ~3. Most bright
galaxies are at z <= 0.2.
,
the change in the wavelength over the wavelength itself. For
very distant objects, the expansion of the universe causes a lengthening
in the wavelength of light we see; a longer wavelength means a
shift towards the red end of the spectrum, hence redshift. The
most distant galaxies we observe are at z = ~3. Most bright
galaxies are at z <= 0.2.
Mass. The astronomical unit of mass is that of the Sun,
a solar mass, or Mu.
A galaxy like the Milky Way contains ~1011 Mu
of luminous matter. Galactic satellites typically contain ~108
Mu.
Brightness. The surface brightness of a spiral galaxy's
disk is well fit by the exponential function, I(R) = I0
exp(-R/Rd). Thus the scale length, Rd,
is a radius at which the surface brightness drops off by about
60%. An isophote is a contour of equal surface brightness.
Because the edges of galaxies are fuzzy and dim, we specify their
spatial extent by the Holmberg radius, or RHo. RHo
is defined as the 26.5 mag/arcsec2 isophote; this is
the faintest light that terrestrial based telescopes can reliably
measure.
Abbreviations. HI is neutral atomic-hydrogen gas. When
capitalized, the Galaxy refers to our galaxy, the Milky
Way. The abbreviation LMC stands for the name of the Milky
Way's largest satellite, the Large Magellanic Cloud; similarly
SMC for the Small Magellanic Cloud. An abundant type of
small, dim galaxies are known as dwarf spheroidals, or dSph
galaxies.
§C. A Review
of Gravitation
Stars are very small in comparison to the size of a galaxy. In
a galactic disk 30 kpc across and 1 kpc thick, even 1011
stars like the sun each possess ~2.1 x 1041 km3
of space -- a volume over 5 x 1022 times the volume
of the star itself. Scaled to the size of a person, that is a
sphere half the size of Jupiter, roughly five times the size of
Earth -- an enormous volume. While stars are not uniformly distributed
within galaxies, the time between stellar interactions is of order
1019 yr. (Binney & Tremaine 1987), much longer
than the age of the universe. Thus stellar collisions are rare
and consequently unimportant to the evolution of a galaxy; this
is known as a collisionless system. In a collisionless
system, the precise location of particles is unimportant, the
system primarily evolves under the influence of the mean density.
The evolution of such a system is as follows. Using Newton's
law of gravitation
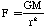 ,
(C-1)
,
(C-1)
we can express the force at a position x from a distribution
of material, by summing the individual contributions to the total
force from each particle located at x',
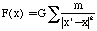 .
(C-2)
.
(C-2)
The equivalent integral form for each element of mass (x')
3x' located at x' (in a continuous distribution,
(x') is the density at x'), is
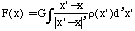 .
(C-3)
.
(C-3)
If we the define the gravitational potential (x) as
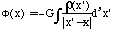 ,
(C-4)
,
(C-4)
then the force at a specific point x is just
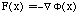 .
(C-5)
.
(C-5)
The equations of motion of a collection of self-gravitating particles
is the collisionless Boltzmann equation. In practice, the Boltzmann
equation is difficult to solve directly, therefore an N-body technique
is used. The continuous phase-space distribution is sampled at
N points, providing a finite ensemble. The ensemble provides
an estimation for the system's density, and thereby its potential.
The evolution of this ensemble is then governed by Newton's laws
of motion
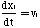 ,
(C-6)
,
(C-6)
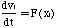 ,
(C-7)
,
(C-7)
where F(xi) is given by Equation C-5. The accuracy
of the ensemble is improved by increasing N, sampling at more
points. The continuum limit is obtained as N -> Inf. The specific
particle techniques are addressed in §4.1.
§D. Dynamical
Friction
The Chandrasekhar dynamical friction
formula (Chandrasekhar 1943) is:
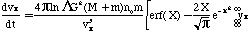
where X M/(2), n0 is the total number density
of stars. In the limit M >> m, as in the case of
a satellite galaxy or globular cluster moving through a galaxy's
halo, this formula illustrates two important characteristics of
dynamical friction. First, the frictional drag is proportional
to the local mass density (n0m) but independent
of the specific mass m.. We can replace n0m
with the overall background density , obtaining an equivalent
formula valid for a spectrum of different background masses,
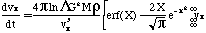 (M >>
m).
(M >>
m).
Secondly, because the frictional acceleration is proportional
to M, the frictional force is proportional to M2 (e.g.:
F = Ma). As the mass M travels through the halo, it deflects
matter such that it creates an overdensity of matter behind it.
The amplitude of this overdensity is proportional to M and the
gravitational force that it exerts on the mass is proportional
to M times the amplitude, or M2.
This overdensity is precisely the gravitational wake discussed
by Mulder (1983). Because the wake's self-gravity is neglected
in the Chandrasekhar approximation, simulations with reactive
halos may react differently than those with fixed halos due to
the generation and evolution of the wake.
In this paper's model, the satellites fail to pass sufficiently
deep that an obvious wake appears. Simulation models with extended
halos or a greater number of halo particles may reveal wake characteristics.
§E. Static
Force on a Motionless Ring
Problem: Determine the force from a mass Ms,
placed along the x-axis a distance R from the origin upon
a center-fixed ring of total mass Mr and radius
r. Ms is a height h above the
x-y plane. The distance d from the mass to the edge of
the ring may be found by examining the system's geometry.
A) Top View
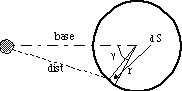
dist2 = base2 + r2 - 2 r base
cos() (E-1)
dS = r d (E-2)
B) Side View
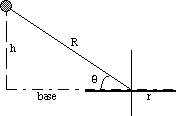
h = R sin() (E-3a)
base = R cos() (E-3b)
C) Final View
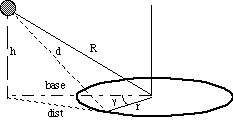
d2 = h2 + dist2 (E-4)
The distance d from the mass to the edge of the ring is
found by combining the geometrical equations.
dist2 = base2 + r2 - 2 r base
cos() (eqn E-1)
h = R sin() (eqn E-3a)
base = R cos() (eqn E-3b)
d2 = h2 + dist2 (eqn E-4)
Taking Eqn E-1 and substituting, we find
d2 = R2 sin2 () + base2
+ r2 - 2 r base cos()
= R2 sin2 () + R2 cos2
() + 2 r cos() cos()
= R2 [sin2 () + cos2 ()] +
2 r cos() cos()
d2 = R2 + r2 - 2 r cos() cos()
(E-5)
The gravitational force from Ms upon a small
portion of ring dm is
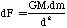
In a uniform ring of mass Ms and radius r,
= Mr / 2r
dm = dS
Therefore,
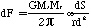
From Eqn E-2,
dS = r d
Thus,
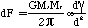
The force on the entire ring is then
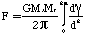 (E-6a)
(E-6a)
or, inserting Eqn E-5,
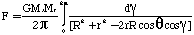 (E-6b)
(E-6b)
integrated about the ring.
As the ring is center-fixed and the mass taken to lie upon the
x-axis, the force acts only in the direction of the z-axis, rotating
the ring along the y-axis. The angle of inclination of the mass
above the plane, , is assumed fixed, but will decrease as the
ring tips.
Fz is the z-axis projection of F, or
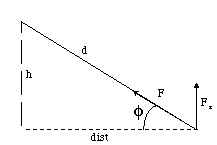
Fz = F sin = F h/d (E-7)
therefore combining Eqn E-6a and E-7,
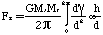 (E-8)
(E-8)
From Eqn E-3a,
h = R sin()
substituted into Eqn E-8, and inserting the extended value for
d from Eqn E-5,
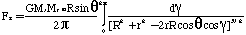 (E-9)
(E-9)
In terms of ring rotation, the force is symmetric about the x-axis;
it's also positive for all negative x and negative for all positive
x. The angular position is set to zero on the y-axis. Thus
the total rotational force is,
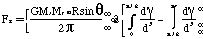 (E-10)
(E-10)
[an error occurred while processing this directive]
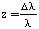 ,
the change in the wavelength over the wavelength itself. For
very distant objects, the expansion of the universe causes a lengthening
in the wavelength of light we see; a longer wavelength means a
shift towards the red end of the spectrum, hence redshift. The
most distant galaxies we observe are at z = ~3. Most bright
galaxies are at z <= 0.2.
,
the change in the wavelength over the wavelength itself. For
very distant objects, the expansion of the universe causes a lengthening
in the wavelength of light we see; a longer wavelength means a
shift towards the red end of the spectrum, hence redshift. The
most distant galaxies we observe are at z = ~3. Most bright
galaxies are at z <= 0.2.
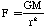 ,
(C-1)
,
(C-1)
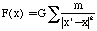 .
(C-2)
.
(C-2)
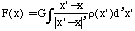 .
(C-3)
.
(C-3)
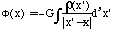 ,
(C-4)
,
(C-4)
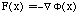 .
(C-5)
.
(C-5)
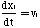 ,
(C-6)
,
(C-6)
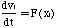 ,
(C-7)
,
(C-7)
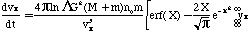
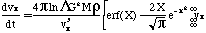 (M >>
m).
(M >>
m).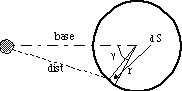


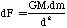
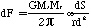
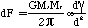
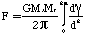 (E-6a)
(E-6a)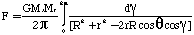 (E-6b)
(E-6b)
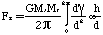 (E-8)
(E-8)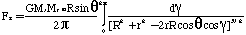 (E-9)
(E-9)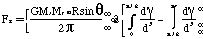 (E-10)
(E-10)